Sehr geehrte Statistic-Trader und Traderinnen,

in dieser Artikelreihe wollen wir ein sehr beliebtes Thema der Trading-Szene behandeln: Die Analyse von Gaps. Höchstwahrscheinlich weiß jeder von Ihnen was ein Gap ist, für die die es nicht wissen, ein Gap ist eine Kurslücke zwischen Schlusskurs und einem Eröffnungskurs.

Die meisten Analysen die wir im Netz gelesen haben, bieten zwar Statistiken zu diesem Thema an, aber nicht unbedingt Schlussfolgerungen oder Zusammenhänge. In dieser Artikelreihe werden wir sowohl den Dax, als auch die US-Märkte auf Kurslücken untersuchen und Ihnen auch Informationen zur Verfügung stellen, die Sie so vielleicht noch nicht in anderen Gap-Analysen gelesen haben.

Wir werden Gaps auf Korrelationen und Saisonalitäten untersuchen und versuchen herauszufinden, welche Parameter dabei helfen können ein gutes Gap-System zum traden aufzubauen und ob es überhaupt möglich ist ein gutes Filter-System für Kurslücken zu entwickeln.

Warum brauchen wir noch eine Gap Analyse?

„Gap Analysen gibt es doch wie Sand am Meer“, dies war der erste Satz als wir über den neuen Content nachdachten. Und das stimmt auch! Doch stellt sich schnell die Frage wie zuverlässig diese durchgeführt worden und was all diese Analysen gemeinsam haben? Hier merkt man schnell, dass sich niemand wirklich Gedanken gemacht hat und lediglich die Wahrscheinlichkeit eines Gaps dokumentiert hat.

Mit dieser Content-Artikelreihe möchten wir Ihnen Gap-Statistiken und Analysen vorstellen, aus der Sie wirklich Nutzen ziehen können und sich, wenn dieses von Ihnen gewollt ist, auch stabile Handelssysteme darauf aufbauen können.

Die Datengrundlage und Analyseparameter

Als Analyse Plattform dient Tradesignal Terminal, die Analyse bezieht sich auf den FDax (also dem Future) und die Daten liefert ebenfalls Tradesignal. Unser Test beginnt am 21.11.2005 und endet am 27.02.2017, was genau 2844 Handelstagen entspricht.

Damit ist eine statistische Relevanz der Untersuchungsmenge gegeben.

Wir messen hierbei den Unterschied zwischen dem Schlusskurs und dem Eröffnungskurs des nächsten Tages und runden auf Ganze und halbe Zahlen auf/ab. Damit die Analyse keiner subjektiven Wahrnehmung unterliegt haben wir das Ganze in Equilla programmiert und durch einen Algorithmus laufen lassen.

Denn wenn Sie händisch Systeme oder Markt-Anomalien testen, dann ist es immer von besonderer Wichtigkeit, dass Sie 100% objektiv bleiben. Bei einem händischen Test besteht immer die Gefahr, dass der Analyst sich selbst belügt wenn manche Erkenntnisse zu einem verschlechterten Ergebnis führen würden.

Häufige Thesen

Immer wieder werden Aussagen getätigt wie:

• Ein Long-Gap ist wahrscheinlicher, weil der Index einen positiven Drift hat.
• Ein Long-Gap ist größer als ein Short-Gap.
• Die Gap-Größe steigt im Verhältnis zum Indexwachstum.

Dieser Thesen sowie noch einiger weiterer, werden wir uns nach der „Basis-Analyse“ annehmen.

Die Gap-Statistik

In den 2844 Handelstagen gab es insgesamt 2774 Gaps, was einer Gap Wahrscheinlichkeit von 97,54% entspricht.

Was erstmal überraschend viel klingt ist in der Praxis jedoch relativ harmlos. Denn ein Gap entsteht ja bereits bei einer Kurslücke von 0,5 Punkten und wird dementsprechend von den meisten überhaupt nicht wahrgenommen. Lassen Sie uns deswegen die Gaps in jeweils 10 Punkte Gruppen einteilen (also 0,5-9,5; 10-19,5 usw…). Dann können wir sehen welche Gruppe wie häufig auftritt und wie wahrscheinlich dies ist.

Aus den unteren Abbildungen können Sie sowohl die Anzahl der gesamten Gaps zu den dazugehörigen Punkten entnehmen und Sie können auch die Wahrscheinlichkeiten für das Auftreten solch eines Gaps ablesen.

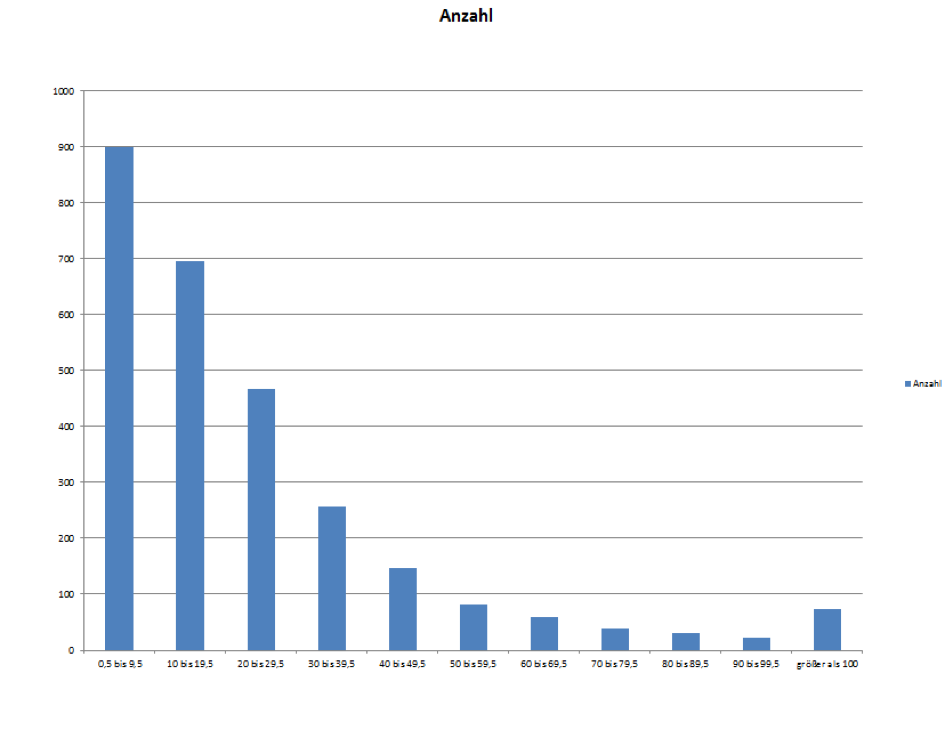(Abbildung 1: absolute Häufigkeiten)

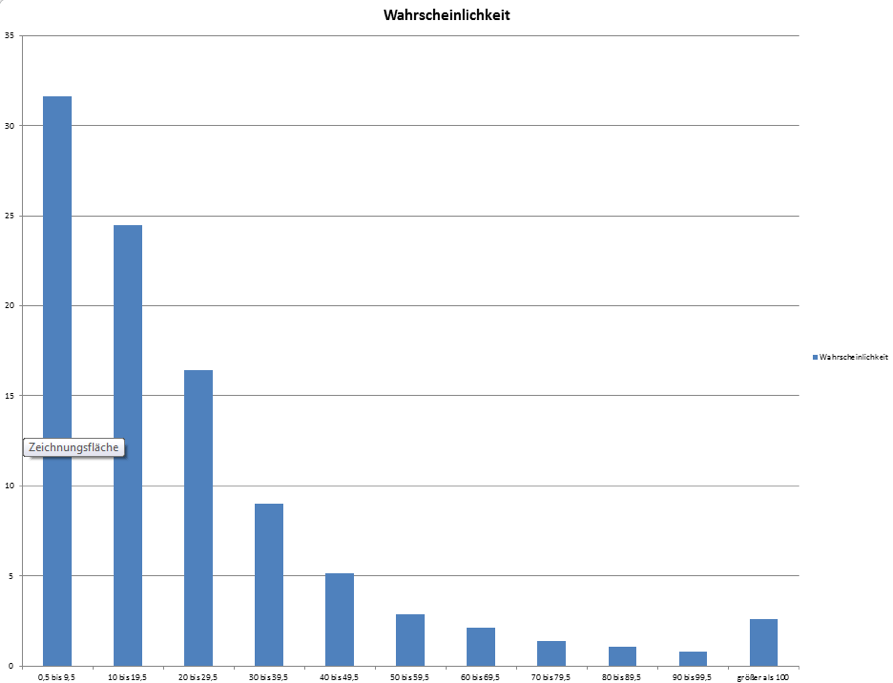(Abbildung 2: Wahrscheinlichkeiten)

Aus den Daten können wir nun den Durchschnnitt sowie den Median ermitteln.

Doch wie wird der Median ermittelt? Der Median ist genau wie das arithmetische Mittel (Durchschnitt) ein Mittelwert. Doch werden beim Median nicht alle Werte, wie beim normalen Durchschnitt, berücksichtigt. Der Median erstellt, um es zu verdeutlichen, 2 gleichgroße statistische Listen. Auf der linken Seite finden sich die kleineren Werte und auf der rechten Seite die größeren. Der Median ist dann der Wert, der von ALLEN Werten genau in der Mitte liegt. Als Beispiel: Wir haben eine Datenmenge von 9 Gaps. Hier die 9 Beispiel-Daten: 10,20,56,50,2,199,350,18,33.

Wir denken, dass Sie alle wissen wie Sie ein arithmetisches Mittel (Durchschnitt) errechnen. Sie summieren alle 9 Daten und dividieren diese durch die Anzahl der Daten. In diesem Fall erhalten wir 738/9 = 82. Somit haben wir ein durchschnittliches Gap von 82 Punkten.

Wie kommen wir nun zum Median? Wenn Sie Excel oder andere Spreadsheet-Programme verwenden, dann können Sie diesen einfach mit einer Formel errechnen (in Excel z.B. mit =MEDIAN).

Doch machen wir das mal Old-School. Sie ordnen nun alle Werte der Größe nach. Somit haben wir folgende Reihenfolge: 2,10,18,20,33,50,56,199,350. Der Median ist somit 33 Punkte, da die 33 die mittigste Zahl der Reihenfolge ist. Hier nochmal für die Leute die die Formel wissen wollen wie Sie ein Median bei geraden oder ungeraden Zahlenfolgen errechnen:

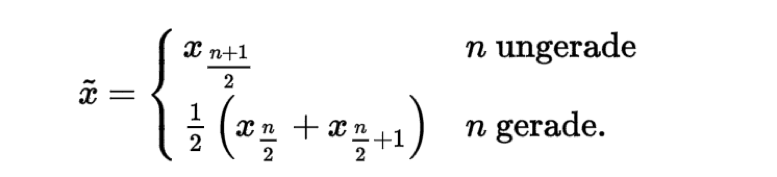(Abbildung: Wikipedia.de)

Während das durchschnittliche Gap eine Größe von 25,25 Punkten aufweist, liegt der Median lediglich bei 16,5 Punkten. Wieso geben wir hier zwei Werte an? Ganz einfach, der Median ist robuster gegenüber von Ausreißern wie Beispielsweise dem Brexit Gap. Solche Ausreißer werden jedoch im Durchschnitt berücksichtig, welche der beiden Werte Ihnen lieber ist können Sie selbst entscheiden. So viel zur Standartanalyse.

Die verbreitetsten Thesen

Hier nochmal die Thesenübersicht:

• Ein Long-Gap ist wahrscheinlicher, weil der Index einen positiven Drift hat.
• Ein Long-Gap ist größer als ein Short-Gap.
• Die Gap-Größe steigt im Verhältnis zum Indexwachstum.

Kommen wir nun zur 1. These.

Diese besagt, dass ein Long-Gap häufiger auftritt aufgrund des positiven Driftes des Indexes. Zwar sind statistisch gesehen 52,27% der Gaps in Richtung long (1450 Up Gap’s zu 1324 Down Gap’s), doch dies ist viel zu wenig um statistisch signifikant zu sein. Die Visualiserung der Analyse erkennen Sie im unteren Bild.

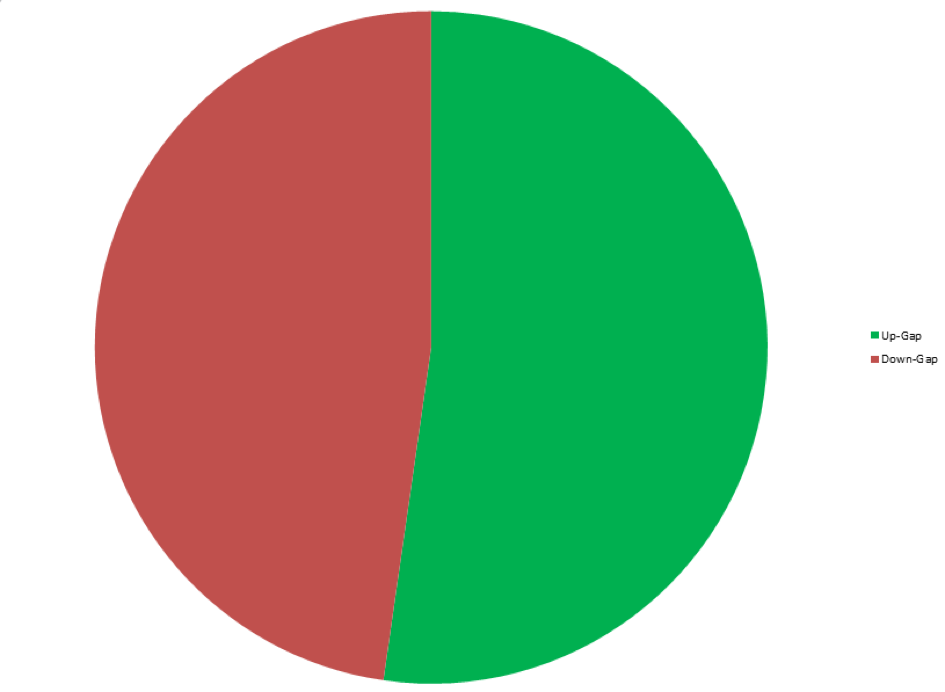
(Abbildung 4)

Wie sieht es aber nun mit der zweiten These aus? Ist ein Long Gap wirklich größer als ein Short Gap? Statistisch gesehen beträgt ein durchschnittliches Long Gap 24,16 Punkte, während ein durchschnittliches Short Gap 26,44 Punkte beträgt und somit sogar um 8,63% größer ausfällt. Rechnen wir nun die Gap Größen und die Gap Anzahl der Up- und Down-Gaps zusammen und dividieren diese durcheinander kommt interessanter Weise der Faktor 1,00068595 raus.

Dies bedeutet, dass die Down Gap’s um denselben Faktor größer sind wie die Long Gap’s häufiger.

In der gemessenen Zeit sind maximal 9 Up Gaps und 8 Down Gaps aufeinander gefolgt, auch hier kein signifikanter Unterschied.

Was ist nun mit der 3. These? Was logisch klingt ist allerdings falsch. Nehmen wir hier einfach den Zeitraum vom 21.11.2005 bis zum 27.02.2017 und berechnen den Korrelationskoeffizienten. Dieser liegt bei 0,046897, damit ist eine Korrelation zwischen Indexstand und Gap Größe widerlegt.

Was besagt ein Korrelationskoeffizient und die Zahl 0,046897? Man verwendet einen Korrelationskoeffizienten um einen möglichen linearen Zusammenhang erklären zu können. Ein Korrelationskoeffizient kann immer nur zwischen -1 und 1 liegen. Haben wir eine Korrelation von -1, so bedeutet das, dass wenn der eine Wert um einen Punkt steigt, der andere Wert genau um einen Punkt sinkt. Haben wir eine Korrelation von 1, so heißt das, dass der eine Wert um eins steigt und der andere Wert auch um eins steigt. Somit ist -1 eine negative Korrelation und +1 eine positive Korrelation. Haben wir den Korrelationskoeffizienten von 0, so liegt keine nachweisliche Korrelation vor.

Zurück zu unserer These. Wir haben untersucht, ob die Gap-Größen größer werden, weil der Dax-Stand auch größer wird oder ob dies nur durch selektive Wahrnehmung so aufgenommen wird?

In diesem Fall haben wir eine Korrelation von 0,046897 und somit keine signifikante Aussage über eine Korrelation für solch eine These. Somit können wir die These verneinen.

Dax/Gap Saisonalität

Die These: Die Saisonalitäten des Dax korrelieren mit dem Auftreten von Gaps in die selbige Richtung.

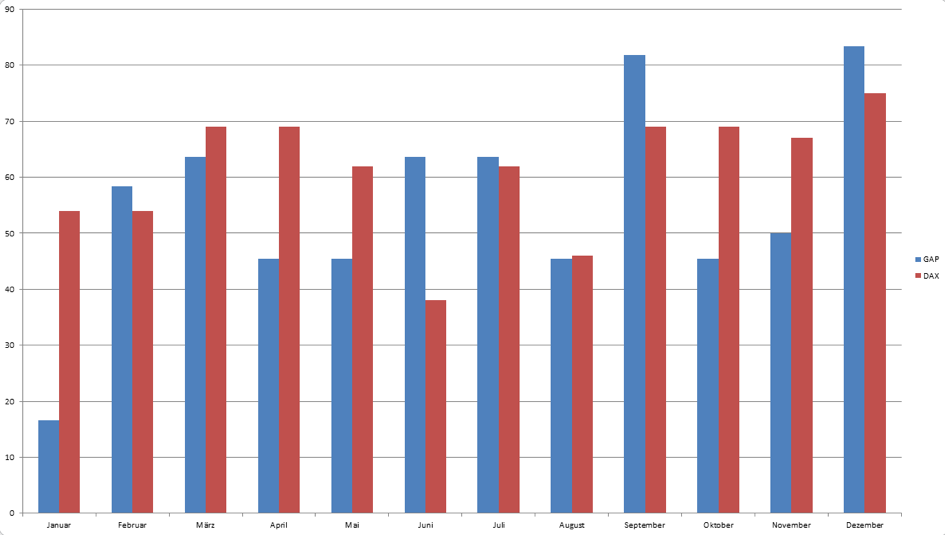(Abbildung 5: Quelle Dax Saisonalität http://stockcharts.com/freecharts/seasonality.php?symbol=%24DAX)

Dafür werden im Dax die Monate gezählt in denen er höher schließt, sowie die Monate in denen Gaps mehr Punkte Long gemacht haben als Short. Selbstverständlich berechnen wir dafür wieder den Korrelationskoeffizienten um zu schauen ob, und wenn ja, wie stark diese Werte korrelieren. Dieser liegt bei 0,311368 und sagt damit aus, dass keine statistisch signifikante Korrelation vorliegt.

In Teil 2 werden wir uns mit dem Verhältnis von der Bewegung und der möglich entstehenden Gap-Größe beschäftigen. Wenn Sie keinen Teil verpassen wollen, dann tragen Sie sich einfach in unseren kostenlosen Newsletter ein.

Wir wünschen Ihnen ein erfolgreiches Trading!

Ihr Statistic-Trading Team